حل المعادلات التربيعية باستعمال القانون العام وقانون المميز | تمارين محلولة

بكل تأكيد قد تحتاج في حياتك الدراسية إلى معرفة حل المعادلات التربيعية ^[1] باستعمال القانون العام وفهمها بالتفصيل حتى تتمكّن من اجتياز أي معادلة تصادفك في التمارين العملية. إن بحثت مليّاً عن ذلك ولن تجد شرح كافٍ حول هذا الموضوع، تابع معنا سطورنا القادمة المقدّمة لك شرح تفصيلي مدعّم بالأمثلة مع الحل.

المعادلات التربيعية (من الدرجة الثانية)

تم تسمية هذه المعادلات بالتربيعية لأن الأس الأكبر في حدودها من المرتبة الثانية أي أنه أس تربيعي 2 محمول على المجهول “المتغيّر” كالآتي x². هناك أكثر من طريقة لحل المعادلات التربيعية مثل:

• طريقة التحليل إلى عوامل.
• طريقة إكمال المربع (الإتمام إلى مربع كامل).
• طريقة الجذر التربيعي.
• وطريقة القانون العام بالمميز.

كل هذه الطرق استطرقنا لشرحها بشكل كافٍ ومفصّل مع الأمثلة التوضيحية في مقال سابق يشرح حل المعادلات من الدرجة الثانية، إلّا أن هناك طريقة أخرى تدعى بحل المعادلات التربيعية بيانيا أي يمكنك معرفة مجموعة حلول المعادلة من التمثيل البياني، ولكن قد تعطي هذه الطريقة حلول غير دقيقة. ما نريد تسليط الضوء عليه اليوم بشكل أكثر تفصيلاً في هذا المقال هو حل المعادلات التربيعية باستعمال القانون العام “المميز”.

حل المعادلات التربيعية باستعمال القانون العام

إن هذه الطريقة هي الطريقة الأكثر استعمالاً، ولكنها قد تأخذ إجراءات أطول من باقي الطرق إلّا أنها فعّالة لجميع أشكال المعادلة. كما أن الشكل العام للمعادلة هو كالآتي:

ax² + bx + c = 0

• a ، b ، c قيم معلومة.
• a معامل المجهول x².
• b معامل المجهول x.
• c حدّ ثابت “مطلق”.

نستطيع حل المعادلات التربيعية باستعمال القانون العام على النحو الآتي “صيغة القانون العام”:

x = (- b ± √(b² – 4ac)) / 2a

• حيث أن a ≠ 0، وذلك حتى لا ينعدم المقام.
• والمقدار b² – 4ac ≥ 0، لأن هذا المقدار بالكامل تحت الجذر التربيعي.

كما أن بتطبيق هذا القانون العام، تتمكّن من معرفة قيم حلول “جذور” المعادلة التي تجعل المساواة صحيحة.

تمارين على قانون حل المعادلة التربيعية العام مع الحل

مثال 1: حل المعادلة التربيعية الآتية باستعمال القانون العام:

 3x² – x = 6 •

الحل:

• أولاً، علينا كتابة المعادلة التربيعية بالشكل العام ax² + bx + c = 0 لحل المعادلات التربيعية باستعمال القانون العام، ويتم ذلك بنقل العدد 6 إلى الطرف الآخر مع الانتباه إلى تغيير إشارته، أو يمكن الوصول إلى الشكل العام بأسلوب صحيح آخر عن طريق طرح العدد 6 من طرفي المعادلة. أي ممكن مباشرةً نقل العدد 6 والوصول إلى الشكل العام وفق الآتي:

3x² – x – 6 = 0

أو طرحه من طرفي المعادلة للوصول إلى الشكل العام:

3x² – x – 6 = 6 – 6

3x² – x – 6 = 0

• ثانياً، علينا تحديد القيم المعلومة وفقاً للمعادلة:

a = 3 ، b = -1 ، c = -6

• ثالثاً، نقوم بتطبيق القانون العام بشكل مباشر بتعويض قيم a و b و c.

صيغة القانون العام: x = (- b ± √b² – 4ac) / 2a

x = (- (-1) ± √((-1)² – 4(3)(-6))) / 2(3)

x = (1 ± √(1 +72)) / 6  »   x = (1 ± √73) / 6

• بعد ذلك، نجد أن للمعادلة حلّان مختلفان وهما:

x1 = (1 – √73) / 6

x2 = (1 + √73) / 6

إذاً، مجموعة جذور ” حلول” المعادلة هي:

S { (1 – √73) / 6 ، (1 + √73) / 6 }

كما يمكنك تبسيط الحل بشكل تقريبي باستخدام الآلة الحاسبة لتجد أن:

x1 = (1 – √73) / 6 = – 1.25

x2 = (1 + √73) / 6 = 1.6

مثال 2: حل المعادلة التربيعية باستخدام القانون العام

 x² – 5x – 2 = 0 •

الحل:

• أولاً، نحدّد القيم: a = 1 ، b = -5 ، c = -2
• ثم نعوّض مباشرةً في القانون العام لحل المعادلات التربيعية:

صيغة القانون العام:

x = (- b ± √(b² – 4ac)) / 2a » x = (- (-5) ± √((-5)² – 4(1)(-2))) / 2(1)

x = (5 ± √(25 + 8)) / 2(1) » x = (5 ± √33) / 2

• بعد ذلك نحصل على الحلّين:

x1 = (5 + √33) / 2

x2 = (5 – √33) / 2

كما يمكننا كتابة مجموعة جذور ” حلول” المعادلة على الشكل:

S { (5 + √33) / 2 ، (5 – √33) / 2 }

مثال 3: أوجد حل المعادلة التربيعية الآتية باستعمال القانون العام:

 2x² – 5x + 2 = 0 •

الحل:

• أولاً، نحدّد القيم: a = 2 ،  b = -5 ، c = 2
• ثم نعوّضها بشكل مباشر في القانون العام لحل المعادلات التربيعية من الدرجة الثانية:

x = (- b ± √(b² – 4ac)) / 2a » x = (- (-5) ± √((-5)² – 4(2)(2))) / 2(2)

x = (5 ± √(25 – 16)) / 4 » x = (5 ± √9) / 4

• ثم نعزل الحلول:

x1 = (5 + 3) / 4 = 2

x2 = (5 – 3) / 4 = 1/2

كما يمكننا كتابة مجموعة جذور ” حلول” المعادلة على الشكل الآتي:

S { 2 ، 1/2 }

قانون المميز في الرياضيات لحل المعادلة التربيعية

يمكنك في حل المعادلات التربيعية باستعمال القانون العام، أن تعرف عدد الحلول الممكنة للمعادلة قبل الشروع بحلها، وذلك من خلال إخراج صيغة المميز دلتا Δ أو ممكن القول قانون المميز لحل المعادلة التربيعية من صيغة القانون العام. قانون المميز هو المقدار الواقع تحت الجذر التربيعي في القانون العام ألا وهو:

Δ = b² – 4ac

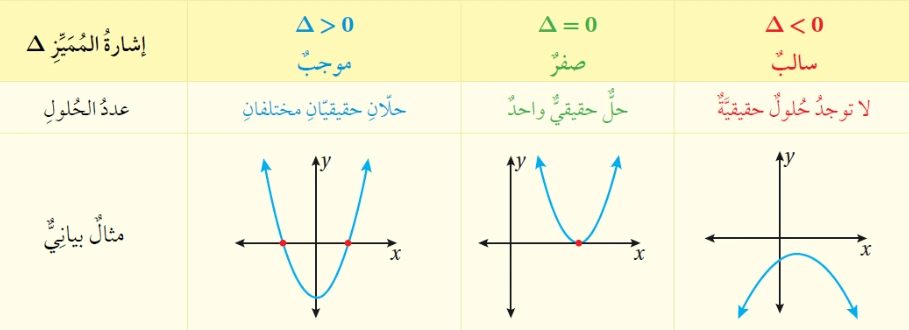
تستطيع استعمال قانون المميز لتحديد عدد الحلول الممكنة في حل المعادلات التربيعية باستعمال القانون العام، وذلك بتعويض القيم المعلومة a و b و c في قانون المميز، وبعد ذلك نميّز ثلاث حالات:

• إذا كانت Δ > 0 أي أن إشارة المميز دلتا موجبة » للمعادلة حلّان حقيقيان مختلفان وهما:

x1 = (- b + √Δ) / 2a •

x2 = (- b – √Δ) / 2a •

• أمّا إذا كانت Δ < 0 أي أن إشارة المميز دلتا سالبة » المعادلة مستحيلة الحل أي ليس لها حلول ” جذور” في مجموعة الأعداد الحقيقية.
• وإذا كانت Δ = 0 أي أن قيمة المميز دلتا مساوية للصفر » للمعادلة حلّان متماثلان أي يمكن القول حل وحيد “مضاعف” وهو:

(x = – b / (2a •

الصورة المدرجة أعلاه تبيّن حالات المميز وفق التمثيل البياني إن أردت الاطّلاع على المخططات البيانية، كما تعرف بحل المعادلات التربيعية بيانيا.

تمارين على قانون المميز لحل المعادلة التربيعية مع الحل

مثال 1: أوجد حل المعادلة باستعمال قانون المميز لحل المعادلة التربيعية:

x² – 6x = -9 •

الحل:

• أولاً، نكتب المعادلة بالشكل العام: ax² + bx + c = 0

x² – 6x + 9 = 0

• نحدّد القيم: a = 1 ، b = -6 ،  c = 9
• ثم نكتب قانون المميز لحل المعادلة التربيعية من القانون العام: Δ = b² – 4ac
• ثم نعوّض قيم a ، b ، c في قانون المميز من المعادلة المعطاة كالآتي:

Δ = (-6)² – 4(1)(9) » Δ = 36 – 36 = 0

• نجد أن Δ = 0 أي أن للمعادلة حلّان متماثلان ( حل وحيد مضاعف) وهو:

 x = – b / (2a) = – (-6) / 2 (1) = + 6 / 2 = 3

إذاً، جذر “حل” المعادلة هو: S { 3 }

مثال 2: أوجد حل المعادلة التربيعية بالمميز:

x² – 4x + 5 = 0 •

الحل:

a = 1 ، b = -4 ، c = 5

صيغة المميز: Δ = (-4)² – 4(1)(5) « Δ = b² – 4ac

» Δ = 16 – 20 = – 4

نجد أن Δ < 0 أي أن دلتا سالبة، وبالتالي المعادلة مستحيلة الحل ليس لها أية جذور حقيقية.

مثال 3: أوجد حل المعادلة التربيعية باستخدام القانون العام بالمميز:

2x² – 5x + 2 = 0 •

الحل:

• في البداية نحدّد القيم: a = 2 ، b = -5 ، c = 2
• ثم نعوّض في قانون المميز لتحديد عدد حلول المعادلة: Δ = b² – 4ac

9 = Δ = (-5)² – 4(2)(2) « Δ = 25 – 16 «

• نجد أن Δ > 0 أي أن قيمة المميز دلتا موجبة، وبالتالي للمعادلة حلّان مختلفان وهما:

x1 = (- b + √Δ) / 2a •

x1 = (- (-5) + √9) / 2(2) = ( 5 + 3) / 4 = 2

x2 = (- b – √Δ) / 2a •

x2 = (- (-5) – √9) / 2(2) = ( 5 – 3) / 4 = 1/2

إذاً، مجموعة جذور ” حلول” المعادلة هي:

S { 2 ، 1/2 }

أهم الأسئلة الشائعة حول حل المعادلات التربيعية باستعمال القانون العام

1- كم طريقة لحل المعادلات التربيعية؟

هنالك طرق عديدة لحل المعادلات التربيعية أي المعادلات من الدرجة الثانية:

• حل المعادلة بالتحليل إلى عوامل.
• أو بطريقة إكمال المربع ( الإتمام إلى مربع كامل).
• أو طريقة حل المعادلات التربيعية باستعمال القانون العام وقانون المميز.
• أو باستخدام الجذر التربيعي في حال انعدام الحدّ bx.
• كما هناك طريقة أخرى لكنها غير دقيقة بشكل كافٍ وهي طريقة التمثيل البياني.

2- ما هو القانون العام لحل المعادله؟

صيغة القانون العام على الشكل الآتي:

x = (- b ± √(b² – 4ac)) / 2a

حيث أن المقدار b² – 4ac هو قانون المميز في الرياضيات:

Δ = b² – 4ac

بعد أن قدّمنا إليك في سطور واضحة ومفصّلة طريقة حل المعادلات التربيعية باستعمال القانون العام مع تمارين محلولة، بالإضافة إلى توضيح قانون المميز لحل المعادلة التربيعية وتحديد حلولها، نتمنى أن تكون قد استفدت من هذا المقال وقمت بتجريب الحل بمفردك.

اقرأ أيضاً:

أجمل عبارات للمعلم المتميز 2023