قانون المسافة | شرحه وأمثلة شاملة عنه

المسافة هي مفهوم علمي يستخدم لقياس الفراغ الفاصل بين نقطتين في الفضاء. يتم قياس المسافة بوحدات محددة مثل المتر، الكيلومتر، القدم، الأميال وغيرها من الواحدات. تعتمد واحدة قياس المسافة على الغرض من القياس. حيث يمكن استخدام المتر لقياس المسافة بين نقطتين قريبتين من بعضهما البعض، بينما يمكن استخدام الكيلومتر لقياس المسافة بين مدن مختلفة أو دول. وهنا سنستعرض قانون المسافة وأمثلة عنه.

قانون المسافة والسرعة والزمن

يعطى قانون المسافة بين موقعين أو نقطتين من مكانٍ ما، وبدلالة مفهومي السرعة (v) والزمن (t) بالعلاقة التالية:

المسافة (d) = السرعة (v) × الزمن (t)

حيث أن:

d: هي المسافة المقاسة بين نقطتين مدروستين، ويتم قياسها في الجملة الدولية بواحدة المتر (m).

v: السرعة التي يسير بها الجسم، وتقاس في الجملة الدولية بواحدة متر/ثانية أو (¹−m.s).

t: هو مقدار الزمن المستغرق في قطع هذه المسافة، ويقاس الزمن في الجملة الدولية بواحدة الثانية (s).

وبالتالي يمكن استنتاج قانوني الزمن والسرعة تبعاً للمسافة d وهي:

• السرعة (v) = المسافة (d) / الزمن (t).
• الزمن (t) = المسافة (d) / السرعة (v).

وهذا القانون هو القانون المستخدم لحسابها كمقدار فيزيائي.

أمثلة عملية على قانون المسافة

مثال(1): بفرض أن الطفل يركض بسرعة (5) ¹−m.s، وقد استغرق زمناً قدره (16) ثانية. احسب المسافة التي يقطعها الطفل؟

الحل:

يعطى قانون المسافة كما يلي:

d = v × t

ونقوم بتعويض معطيات السرعة والزمن فنجد:

d = 5 ×16 = 80 m

بالتالي ينتج مقدار المسافة المقطوعة مساوياً لـ 80 متراً.

مثال(2): يقود سائق عربة تبلغ سرعتها 27 km/h، ولمدة مقدارها 10 دقائق. والمطلوب حساب مقدار المسافة مقدراً بالمتر.

الحل: أولاً يجب تحويل السرعة إلى الواحدة الدولية وهي m/s، ولتحويلها نقوم بتحويل الكيلومتر إلى المتر، وتحويل الساعة إلى الثواني كما يلي:

(v = 27 × (1000/3600

ويساوي: v = 7.5 m/s

ثانياً نقوم بتحويل الزمن من واحدة الدقيقة إلى الثواني كما يلي:

t = 10 ×60 = 600 s

بالتالي يتم التعويض في قانون حساب المسافة كما يأتي:

d = v × t = 7.5 × 600 = 4500 m

فالمسافة الناتجة هي 4500 متراً وفق السرعة السابقة.

قانون المسافة في الرياضيات

بحسب قوانين الرياضيات، ينص قانون خاص بالإحداثيات الديكارتية على كيفية حساب المسافة رياضياً بين نقطتين معلومتي الإحداثيات. حيث تعطى المسافة باستخدام الإحداثيات كما يلي:

D = √ (x2 – x1 )² + (y2 – y1)²

حيث أن:

x2: وتمثل فاصلة النقطة المدروسة الثانية.

x1: تمثل فاصلة النقطة المدروسة الأولى.

y2: تعبّر عن ترتيب النقطة المدروسة الثانية.

y1: تعبّر عن ترتيب النقطة المدروسة الأولى.

D: هي مقدار جبري يعبّر عن المسافة بين نقطتين معلومتي الفواصل والتراتيب.

⇐ وهنالك خطوات محددة يمكن من خلالها تحديد المسافة ^[1] عند دراسة نقطتين على مستوي الإحداثيات وهي:

• نعيّن النقطتين A,B في المستوي وذلك عن طريق تعيين الفواصل والتراتيب لكل نقطة على حدة.
• نصل بين النقطتين A وB بواسطة خط مستقيم.
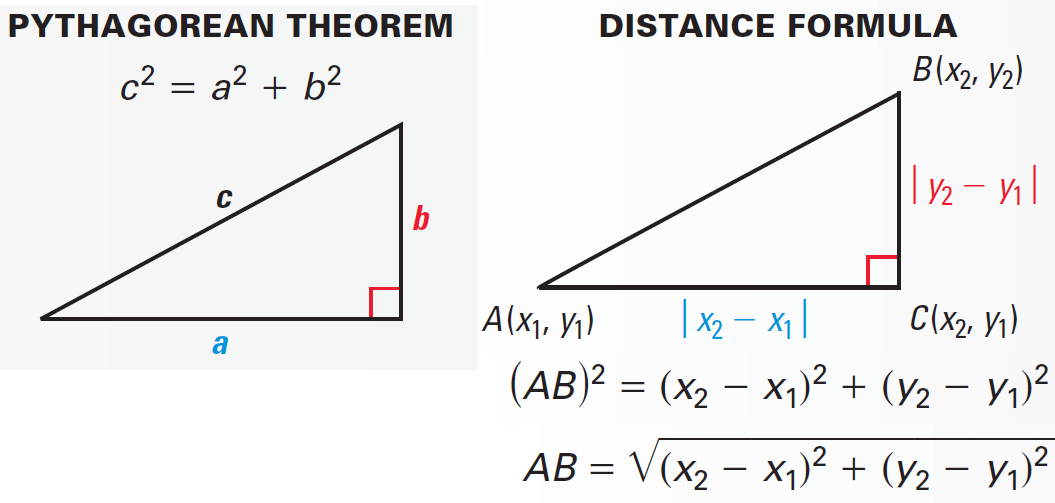
• بعد ذلك نعيّن مستقيمين من كلا النقطتين حتى إكمال الشكل ليصبح مثلث قائم الزاوية في نقطة ثالثة ولتكن C.
• يمثل الآن التباعد بين النقطتين [AB] بالمسافة D وهي طول الوتر في المثلث القائم ABC، ويتم حساب المسافة D باستخدام قانون فيثاغورث. وينصّ على ما يلي:

²(طول الوتر في المثلث القائم) = ²(طول الضلع القائم الأول) + ²(طول الضلع القائم الثاني)

طول الوتر في المثلث القائم = ²(طول الضلع القائم الأول) + ²(طول الضلع القائم الثاني)√

لتوضيح القانون أكثر، سنقدّم عدد من الأمثلة العملية عنه.

أمثلة عملية على قانون المسافة في الرياضيات

مثال: لتكن لدينا النقطتان المفروضتان A,B والتي إحداثياتها على التوالي هي: A(8,6) ، B(10,15). والمطلوب إيجاد مقدار المسافة بالاعتماد على قانونها الديكارتي.

الحل: يتم تطبيق قانون المسافة السابق لحساب مقدار المسافة D بين النقطتين A و B تبعاً للعلاقة التالية:

D = √ (x2 – x1 )² + (y2 – y1)²

نعوض الإحداثيات الخاصة في النقطتين في القانون:

D = √ (10-8)² + (15-6)²

⇐ D = √ (2)² + (9)²

⇐ D = √ 4 + 81

⇐ D = √85

⇐ D = 9.22

حالة خاصة لقانون المسافة (1): حالة نقطة مجهولة

في بعض الأحيان قد تكون المسافة بين النقطتين معلومة، ويطلب منا حساب أحد إحداثيات النقاط المستخدمة في حساب المسافة. وإليك مثالاً عن هذه الحالة:

مثال: أوجد فاصلة النقطة A التي تراتيبها 10، علماً أن إحداثيات النقطة B هي (4,4). وأن المسافة بين النقطتين تساوي المقدار 10.

الحل: لحل هذه المسألة يتم التعويض بالقانون الديكارتي السابق لحساب فاصلة النقطة A:

D = √ (x2 – x1 )² + (y2 – y1)²

⇐ نعوض كما يلي:

10 = ²(x – 4) + ²(10 – 4) √

⇐ 10 = 6² + ²(x – 4) √

نربّع الطرفين فنجد:

⇐ 10² = 6² + ²(x – 4)

⇐ 100 = 36 + ²(x – 4)

⇐ 36 – 100 = ²(x – 4)

⇐ ²(x – 4) = 64

نجذر كلا طرفي المعادلة فنجد:

⇐ x – 4 = 8

⇐ x = 4

حالة خاصة لقانون المسافة (2): حالة نقطة سالبة الإحداثيات

إحدى الحالات الخاصة لإيجاد المسافة اعتماداً على القانون الخاص بالإحداثيات الديكارتية بين النقطتين هو حالة كون أحد النقطتين سالبة الإحداثيات، أي فاصلتها وترتيبها هي عبارة عن قيم سالبة. ولبيان طريقة التعامل مع هذه الحالة إليك مثالاً مفصّلاً عنها:

مثال: لتكن لدينا إحداثيات النقطتين A , B  كالتالي: (6-, A (6,3) , B (-10. والمطلوب هو حساب مقدار المسافة بين نقطتين بالاعتماد على قانونها الديكارتي.

الحل: نقوم بالتعويض مباشرةً بالقانون الخاص بالمسافة التالي:

D = √ (x2 – x1 )² + (y2 – y1)²

D = √ (-10 -6)² + (-6 -3)²

⇐ D = √ (-16)² + (-9)²

⇐ D = √ 256 + 81

⇐ D = √ 337

⇐ D = 18.5

قانون المسافة بين نقطتين في الفراغ

هنالك قانون إضافي لحساب المسافة في حال دراسة نقطتين في الفراغ ^[2] ، حيث أن النقاط في هذه الحالة تكون ثلاثية الإحداثيات، أي كل نقطة تمتاز باحتوائها على (x , y , z). ويمكن توضيح المسافة لنقاط بثلاث إحداثيات كما يلي:

 D = √ (x2 – x1 )² + (y2 – y1)² + (z2 – z1)²

مثال: لحساب المسافة بين نقطتين بالإحداثيات التالية: B(8 ,6 ,6) ، A(3 ,5 ,9) . نعوّض في القانون السابق كما يلي:

D = √ (x2 – x1 )² + (y2 – y1)² + (z2 – z1)²

⇐ D = √ (8 – 3 )² + (6 – 5)² + (6 – 9)²

⇐ D = √ (5)² + (1)² + (-3)²

⇐ D = √25+ 1+ 9

⇐ D = √35

⇐ D = 5.9.

كيف أحسب المسافة بين نقطة ومستقيم؟

لحساب المسافة بين نقطة معطاة إحداثياتها (x1 , y1)ومستقيم بالشكل:

أولاً يجب إعطاء معادلة المستقيم وهي:y = m.x + b 

حيث أن m تمثل ميل المستقيم الموصوف بالمعادلة. ونحتاج في هذه الحالة إلى تحويل المعادلة إلى معادلة طرفها الثاني معدوم. أي تصبح المعادلة بالشكل:

كيف أحسب المسافة بين مستقيمين؟

بنفس الطريقة السابقة، يلزم للحل معادلتي المستقيمين اللازم حساب المسافة بينهما. والشكل الأساسي للقانون المستخدم في هذه الحالة لحساب المسافة هو:

 d = | C2 – C1 | / √A² + B²

وبفرض معادلة المستقيمين سيتم تحويلها للشكل التالي، بحيث ستصبح معادلة المستقيم الأول: A1.​x + B1.​y + C1 ​= 0

ومعادلة المستقيم الثاني: A2.​x + B2.​y + C2 ​= 0

وبإصلاح معادلتي المستقيمين المفروضتين بالشكل: y = m1.​x + b1  للمستقيم الأول

و  y = m2​.x + b2​ للمستقيم الثاني، نجد أن المسافة تصبح:

d = | b2 – b1 | / √ m² + 1

ويجب التنبيه إلى أن المستقيمين عند الحل ينبغي أن يكونا متوازيين لتتحقق المعادلة.

ما هو الفرق بين المسافة والإزاحة؟

هنالك فرق شاسع ما بين المفهوم العام للمسافة والإزاحة. فقد تمّ وصف الإزاحة ^[3] (Displacemant) في علم ميكانيك الحركة بأنها حركة الجسم المقاسة في اتجاه محدّد، وتمثّل أقصر خط مستقيم يصل بين نقطتين معلومتين. وبشكل عام فإن الإزاحة هي مقدار مرتبط بالقيمة والاتجاه، فقد تكون موجبة أو سالبة أو صفر.

أما المسافة (Distance) ^[4] هي مقدار فيزيائي مرتبط بمقدار عددي فقط، دون أن يكون مرتبطاً باتجاه محدد. بالتالي يمكن القول أن المسافة هي مقدار يمثل الحركة الكلية للجسم، أو للمسار المقاس بين نقطتين معلومتين، وهي مقدار موجب.

أسئلة شائعة عن قانون المسافة

1. كيف أحسب المسافة بين نقطتين؟

لحساب مقدار المسافة العددي بين نقطتين معلومتي الإحداثيات، من خلال القانون التالي:

D = √ (x2 – x1 )² + (y2 – y1)²

حيث أن:

x1 ,y1: هي إحداثيات النقطة الأولى.

x2 ,y2: هي إحداثيات النقطة الثانية.

D: المسافة الناتجة وتمثل طول المسار بين النقطتين.

وباستخدام الآلة الحاسبة نضع إشارة الجذر التربيعي أولاً، ثم ندخل الأرقام التي داخل الأقواس ونربعها، وأخيراً نوجد الناتج النهائي.

2. ما هي واحدة المسافة في النظام الدولي؟

إن الواحدة الخاصة بالمسافة في النظام الدولي للقياسات هي المتر m. كما يمكن حسابها بواحدات شائعة أخرى كالقدم أو السنتيمتر أو الكيلومتر أو الميل.

3. هل السنة الضوئية زمن أم مسافة؟

السنة الضوئية هي مقدار عددي مقاس في الفراغ الضوئي المثالي وتساوي: 9.461 × 10¹² كيلومتراً. وتقدّر المسافة التي يقطعها الشعاع الضوئي في الفضاء على مدار عام كامل.

4. كيف أحسب المسافة باستخدام السرعة والزمن؟

يمكن وبكل سهولة حساب المسافة باستخدام السرعة والزمن، ولحلها أولاً نتأكد من أن جميع الواحدات متناسبة، كأن تكون واحدة السرعة بالمتر/ثانية وواحدة الزمن بالثانية إن كان المطلوب هو المسافة بالمتر. أما إن كانت مطلوبة بواحدة كيلومتر فيجب أن تكون السرعة بواحدة كيلومتر/ساعة والزمن بالساعات. ثم نطبق القانون التالي: d = v × t.

5. هل يمكن أن تكون المسافة سالبة؟

المسافة هي مقدار موجب حصراً، لأنها تمثل طول المسار المقطوع بين نقطتين معلومتين.

اقرأ أيضاً:

حل المعادلات ذات الخطوة الواحدة ثالث متوسط رياضيات | تمارين محلولة